Adopting a SQL interface for CockroachDB had an unexpected consequence; it forced us to dabble in language design.
Most developers working with SQL have heard rumors of a SQL standard, pages upon pages of norms and requirements for all SQL compliant dialects to respect. Based on its existence, it’s natural to draw the conclusion that SQL is fully specified and straightforward to implement. A developer need only carefully follow each step laid out in the standard until they arrive at a working database. It’s a lot like building a couch from IKEA. However, in the months following our decision to create a SQL layer on top of our distributed consistent key-value store, we’ve come to realize that this is far from the truth.
SQL does not provide implementation hints and design details are fully left to developer discretion. If this isn’t enough, most modern SQL databases only comply with a subset of the specification, and their implementation decisions diverge in all directions. So while beginning to construct the SQL layer of CockroachDB, we also had to determine how we wanted our flavor of SQL to look.
Our goal was to balance compatibility with other databases with conciseness of our distributed SQL dialect. Specifically, we needed to figure out which parts of the spec we would implement, how we would approach unspecified behavior, and how we would balance robustness with usability and performance. Of all design decisions that this implies, the one that would be hardest to revisit later and which therefore deserved most attention upfront was how we wanted to deal with typing. We knew we wanted to define a straightforward type system, but the question remained: which one?
In this post, we will detail our pre-beta approach to SQL typing in CockroachDB and what prompted a redesign; our evaluation of the Hindley-Milner type system and a vision for its use in SQL; what Rick & Morty (and an older sister named Summer) have to do with the the SQL typing system CockroachDB currently employs; and how a suitable selection of typing rules is essential to query optimization and thus performance.
Table of Contents
Roles of a SQL type system
In general, a type system is a set of rules that determines types for all valid combinations of values and expressions within a program. The application of these rules then becomes the process of semantic analysis, verifying the syntactic structure of provided code. This analysis assigns meaning to a program by determining what needs to be done at run-time, while making sure to reject invalid queries for which computation would not make sense. In a SQL dialect, the type system also performs the role of determining how a query should be evaluated based on the types at play, resolving the desired implementation for overloaded functions and operators.
INSERT INTO foo (float_col) VALUES (‘3.15’ || ‘hello’);
-- this should probably be rejected
INSERT INTO foo (int_col) VALUES (2 + 3.15);
-- this should probably be accepted
-- but what value gets computed by ‘+’?
An additional role specific to SQL is type inference for placeholders. In SQL query protocols, like Postgres’ wire protocol implemented by CockroachDB, it is customary to separate a “query preparation phase”, where a client declares its intent to run a query to the server, and a “query execution phase”, where a previously declared query is run one or more times. In these prepared queries, a client can declare placeholders to be filled during execution. This provides both safety from security vulnerabilities like SQL injection and improved reusability of queries.
For example, a client can prepare the following query, and only provide the two missing parameters during execution:
INSERT INTO Customers (Name, Address) VALUES ($1, $2);
--sometimes also noted “VALUES (?, ?)”
However, the client must be informed which types are to be used to provide values to these parameters, as the types may depend on the database schema. For this reason, the SQL typing system must also infer and report the types of placeholders.
SQL Typing in CockroachDB, pre-Beta
The initial approach for our typing system adopted a simple and commonly used tactic. During type checking of a given query, we first assigned types to all leaves of a syntax tree. For literal values, these types were based on textual representation. For instance, 1 would be assigned the type INT, while ‘str’ would be assigned the type STRING. For column references or other relationship values, types were assigned to the reference’s type. For instance, referencing a column with type FLOAT would type the syntax node as a FLOAT. Once types were determined for all leaves in our syntax tree, the types were then propagated up through the expression tree, resolving intermediate expression types and eventually resolving the types of the query’s root expressions, all in a single pass. All in all, this “bottom-up” approach was simple to implement and easy to reason about.
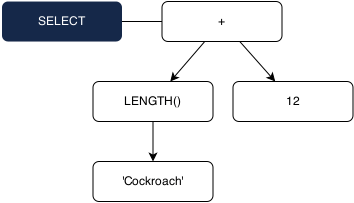
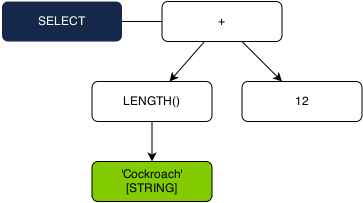
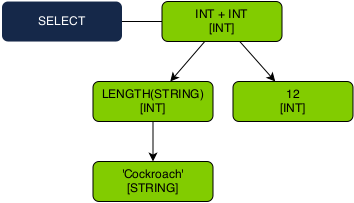
Let’s take a look at how this system works for simple queries. Given the query:
SELECT LENGTH(‘Cockroach’) + 12;
We can first construct a syntax tree that looks like:
With this syntax tree in hand, our next step is to validate that the expression tree (the white nodes) is semantically sound. This is accomplished by traversing the tree and following our “bottom-up” algorithm described above.
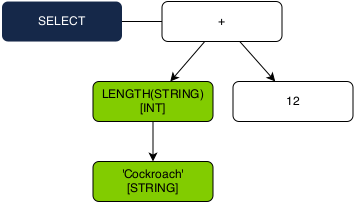
1. Type the ‘Cockroach’ string literal as a STRING.
2. Pick the LENGTH() overload which has a STRING parameter. This overload returns an INT.
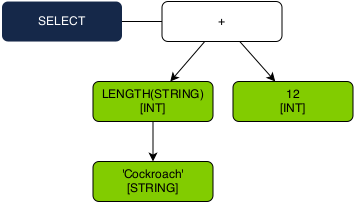
3. Type 12 numeric literal as an INT.
4. Pick the INT + INT operator overload. This overload returns an INT.
5. The SELECT expression tree returns a single INT.
In our pre-beta implementation, placeholders were handled on a case by case basis, depending on how they were used. For instance, if present as argument to a function with only a single overload, a placeholder would receive the type accepted by that function at that argument position. Placeholders providing values for columns in INSERT statements would receive the type of the columns. As children of cast expressions, placeholders would receive a type of STRING. However, for many types of expressions, placeholders were not handled at all.
At the end of this process, we had a working type system that was straightforward and reasonably functional, while still remaining similar enough to other SQL dialects to permit seamless migration in many cases. For the time being, this was sufficient and we were satisfied.
The itch that made us reconsider
Fast forward a few months, and we began to feel discontent with the rigidity of our initial type system. We identified a few distinct limitations that we wanted to address. The first was a limitation caused by the bottom-up analysis, wherein context of an expression was not taken into account when determining the types of expressions. Take for instance:
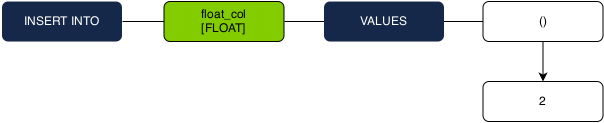
INSERT INTO float_col VALUES (2);
The above would fail during type checking. Let’s take a look at the syntax tree to get an idea of why:
1. Type numeric literal 2 as an INT.
2. The INT type is propagated up as the single value in the VALUES tuple.
3. The INT type cannot be inserted into a FLOAT column, so type checking fails.
In the above example, we created a situation where we had an INT value when we wanted to insert a FLOAT instead. Because of this, our old system would be forced to throw a typing error. The problem was that we were failing to take into account any context when assigning types to the “2” numeric literal, and our system lacked any support for ability to perform implicit type conversions to alleviate this limitation. To get this query to work with the old system, the numeric literal 2.0 was necessary so that it will be typed as a FLOAT and all of the types would “line up”. As this demonstrates, the system often required full explicitness when declaring literal values.
On top of this, some types like DECIMAL and TIMESTAMP were missing literal representations entirely, so the only way to use them as literal values was to use the verbose SQL syntax for explicitly typed literals (name of type followed by value between quotes) or perform a manual cast on the literal values. This meant that a query which used these types would end up looking something like:
INSERT INTO t (dec_col, ts_col) VALUES (DECIMAL ‘1.234’, TIMESTAMP ‘2010-09-28’);
Both our users and colleagues found this a little too verbose.
The next problem was a limited ability to properly determine the types of placeholders, which often resulted in placeholder ambiguity errors from queries that should not be ambiguous. To illustrate this, check out the query
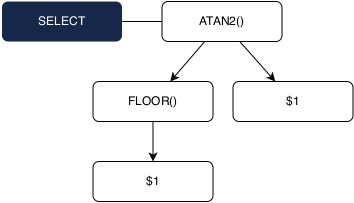
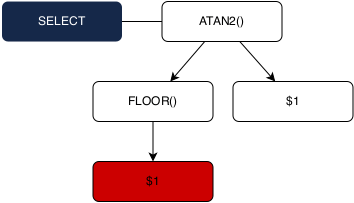
SELECT ATAN2(FLOOR($1), $1);
Attempting to infer the placeholder types during type checking followed the process:
1. Recurse into ATAN2, which has only the single overload of ATAN2(FLOAT, FLOAT).
2. Recurse into FLOOR, which is overloaded for FLOAT and DECIMAL.
3. Because there are multiple overloads for FLOOR, we are unable to determine a type for the $1 placeholder, and therefore throw an ambiguity error.
In this example, the multiple overloads for FLOOR caused an ambiguity which our typing system could not handle. However, a quick examination of this query reveals that the type of placeholder $1 can uniquely be inferred as FLOAT. The logic behind this is that because ATAN2 only takes FLOAT arguments, both $1 and the return value of FLOOR need to be FLOAT types. Since only one overload for FLOOR returns a FLOAT, we can infer that this is the only overload that can be used in this situation. Finally, because the FLOOR overload which returns a FLOAT type also takes a FLOAT type, we can infer that $1 should be typed as a FLOAT.
Unfortunately, our initial type system, with its bottom-up approach, failed to resolve type constraints in a way which would permit such analysis, and as such, we failed to type check the query.
Lastly, we began to feel constrained by a somewhat pessimistic typing of numeric literals. Consider for example:
INSERT INTO float_col VALUES (1e10000 * 1e-9999);
This query would fail during type checking with a complaint that the two numbers do not fit in the FLOAT data type, despite the fact the result after the multiplication would.
While it is important that we exhibit expected overflow behavior and data type range limits when performing arithmetic on dynamic data, there was no pressing reason why we needed to limit arithmetic on numeric literals. We wondered if it would be possible to perform exact arithmetic on all numeric literals, and only face these data type limitations when the literal values needed to be used as a specific data type.
With these limitations in mind, we began rethinking how we could improve the flexibility of our typing system.
Back to school! {#back-to-school}
We knew that the early typing of value literals in the leaves of our expression tree was failing to take into account its surrounding context. To remedy this, we turned towards the literature for type inference [a] [b] [c], which is the automatic deduction of data types within an expression.
Using the literature on type inference in the context of SQL is no small enterprise. Language researchers working on typing traditionally work with some flavor of lambda calculus, where all language features can be expressed as assemblies of function definitions, function application, let bindings (and/or pattern matching), and higher-order function composition. The literature then explains typing in that context, and the exercise of implementation is left to the reader. This is OK for most programming languages where the relationship with lambda calculus is reasonably straightforward, and largely documented already.
In contrast, SQL dialects have largely escaped study of programming language and typing theorists, and it was not immediately clear to us how principles of lambda calculus could be applied to the salient constructs of SQL.
Nevertheless, we started by assuming that SQL semantics could be expressed in the same formalism as the one used by the typing literature, and we began exploring what was out there.
How CockroachDB flew to Hindley-Milner like a moth to the fire
Our original typing algorithm worked in a single “direction,” where the type of each subexpression is fully resolved before moving to its parent. This is too limited, as we explain above, so we wanted to introduce some notion of parent-child collaboration to determine a child expression’s type.
Meanwhile, a few of us had experience with the languages ML, Haskell, and Rust, of which one of the hallmarks is their use of the Hindley-Milner type system [c].
Hindley-Milner (HM) has two key features: it can find the most general type for any part of a program based on its context, and it can do so almost in linear time with respect to the size of the program (as opposed to other iterative typing algorithms which can become quadratically slower as programs become bigger).
We found the idea of applying HM in CockroachDB highly attractive: not only would it make our SQL flavor much more flexible than many other RDBMs, but it would also set a solid foundation for future efforts towards stored procedures and other forms of server-side evaluation of client-provided functions.
In order to use HM in CockroachDB, three steps would be needed:
- We would need to learn how to express the SQL semantics in the lambda calculus formalism
- We would implement this mapping, ie. translate our SQL syntax tree into an intermediate representation (IR) with functional semantics
- We would (re-)implement HM in Go
As we analyzed the technical steps needed to get from here to there, we realized that it would be unwise of us to do this so early in the lifecycle of CockroachDB. First, it would require a lot of work. Second, it may not be needed after all.
The work argument can sound like a cop-out, and to some extent, it is. Expressing SQL in the formal system of lambda calculus and implementing a functional IR actually are on our wishlist, because they will enable us to implement powerful query optimizations. Implementing HM in Go might be a highly unpleasant experience (Go is arguably inadequate for implementing complex pattern matching rules on abstract syntax trees), but it would attract a lot of attention and love from the programming language community. So investing in these work items may actually be the right thing to do in the long term!
However, we also wanted needed to improve the SQL experience of our users in the very short term. While we do have quite a few smart cookies on the team, getting HM to work in CockroachDB in just a few weeks/months in Go would probably require a crew of X-Men instead.
Meanwhile, the stronger argument against implementing HM is that we don’t really need it at this point. Indeed, the power of HM and the motivation behind the complexity of its design is its ability to handle arbitrary algebraic types and higher-order functions properly. Algebraic types in SQL are limited to product types in the form of tuples, and the SQL syntax already clearly delineates when a tuple type is needed and when it is not. So we don’t need extra intelligence to infer tuple types. Moreover, there is no such thing as higher-order functions in SQL, at least, not in our dialect so far!
Applying HM for typing SQL would be unnecessarily heavyweight, at least until a later time when we provide support for custom client-provided functions (i.e. stored procedures or similar) and client-defined types.
Additional peculiarities of typing for SQL
Besides these two main arguments, there was a third argument that made us realise that HM was attractive but not appropriate for CockroachDB after all. For our readers who already have experience with typing systems in other programming languages, this argument may add insight about what makes SQL different. This is one of design trade-offs.
Hindley-Milner, like many type systems, has been designed with the assumption of “compile-once, run-many.” The cost and complexity of type inference and checking, if any, is assumed to be largely offset by the time the program will run, especially when a program is compiled once and ran many times. The client-server architecture of SQL databases and the basic concept of a “SQL query as interface,” in contrast, precludes offsetting the cost of type checking in this way. Even though SQL client/server protocols support a “query preparation” phase run only once for multiple subsequent “query executions,” this is not sufficient.
The main obstacle is that the types in a SQL query depend on the database schema, and the schema can change at arbitrary points in a sequence of query executions. Therefore, a SQL execution engine must re-compute and check types each time a query is reused in a new transaction.
You could suggest here that a cache could help amortize the cost of query analysis, however from our perspective the situation is not so clear: from experience, in SQL it is more likely than other languages that queries are unique and run only one time. In practice, the conservative (and often used) implementation route is to pay the overhead of query analysis for each session anew. This implies a specific extra-functional requirement for SQL type systems not commonly found in other PLs, that their typing algorithm should be relatively lightweight!
Next to performance, another cost trade-off makes SQL distinctly unique as programming languages go: SQL is largely read and written by machines!
HM, like many modern results in programming language theory, has been designed with a human programmer in mind. The flexibility gain in a language equipped with HM is measured by increased productivity of the human programmer: how much less time is needed to write new code and then read and understand existing code, because a powerful type inference algorithms makes programs concise. Furthermore, the ability of HM to find the most general type ensures that a written piece of code is maximally reusable across applications.
In contrast, SQL queries are often assembled programmatically. The trend nowadays is to make SQL largely invisible from the programmers, hidden behind database-agnostic data abstraction layers in application frameworks. These client-side libraries are designed to construct valid, unambiguous SQL queries from the get-go, again and again for each application and use case. Assuming the trend continues, we could even expect these frameworks to become sufficiently intelligent to decide typing client-side and then communicate a fully disambiguated, type-annotated SQL query to the database server. (Granted, we are not there yet, but the argument is not a stretch.) Along the way, we expect to see the amount of work needed by SQL execution engines to analyze queries decrease over time.
To summarize, any effort put into typing for a SQL dialect is intended to aid in raw / command-line use by a DB administrator or for experimentation by the programmers of said client frameworks. The queries written in these contexts are an infinitesimally small proportion of all the queries that reach a SQL server!
In other words, SQL type systems should be just complex (smart) enough to avoid surprising and disgruntling DB admins and framework developers; they do not need to minimize the amount of syntax needed to express all queries that applications may need to use nor maximize the reusability of a query across multiple applications / use cases.
Acknowledging the essentials: starting points for the new design
Considerations about Hindley-Milner notwithstanding, we settled pretty early on the following two requirements for our new typing system.
The first was that the typing algorithm should propagate types from bottom (syntax leaves) to top, as we felt this was a convention least surprising to the majority of our audience. While this requirement would have minimal effect on well-constructed queries, it would vastly improve the usefulness of errors we would be able to provide on poorly-constructed queries.
Following this, we wanted our dialect to continue avoiding implicit type coercions, as our prior programming experience suggests that nothing good comes out of a language that allows them.
Within this framework, the design exercise is restricted in scope to the following specific issues:
- If a function is overloaded, and no overload prototype matches exactly the argument types, what to do? There are two aspects to consider:
- We can’t populate our library with all combinations of overloads that may perhaps make sense (e.g.
float + int,decimal + int,int + float,int + decimal, etc.). If we did so, we would break placeholders: an expression like “1 + $1” would become ambiguous for the type of “$1”. - But then if we only support e.g.
int + intandfloat + float, what to do if the user enters “4.2 + 69” if we also dislike implicit coercions?
- We can’t populate our library with all combinations of overloads that may perhaps make sense (e.g.
- Some SQL functions require “homogeneous types.” For example
COALESCE(x, y, z)is generic on the type of its arguments but require them all to be of the same type. Meanwhile, we felt thatCOALESCE(1, 1.2)orCOALESCE(1, float_col)is well-defined enough that we ought to accept it somehow. The question was how to do this? (Again, without implicit coercions.)
Given our self-selected requirements, we didn’t have a ton of freedom for how to solve these issues. Whenever a sub-expression has a fixed type, for example because it is the name of a table column or the result of a function with a fixed return type, our solution would need to accept this type as a given and either reject or accept the surrounding context based on that type. For example, we knew early on that an expression of the form “float_col + int_col” would be rejected unless we had this specific overload in our library, which we don’t (for now), and that “COALESCE(float_col, int_col)” would be rejected on the same grounds.
However, we are convinced that this limitation is actually a good thing, as it reduces the amount of “magic” in the typing rules and thus the cognitive effort needed for the SQL programmer to understand what is going on.
But then, what remains?
Placeholders
Obviously, placeholders are special and need to “learn from their context”. In a pure bottom-to-top algorithm, an expression of the form COALESCE(int_col, $1) would always be rejected because the recursion would consider $1 in isolation and simply not know what to do with it. So the typing rules must necessarily make a dent on the bottom-to-top principle for placeholders.
Constant Literals
In addition to this, we invested extra effort into constant literals, which are the textual representations of constants in the SQL query source text.
In many “simple” languages like C, C++, Java, ML, and others, constant literals are assigned a type independent of context, based only on their lexical form. For example, “123” receives (or is interpreted using) type INT because it contains only digits and no decimal separator; “123.23” receives type FLOAT because it has a decimal point, and “‘abc’“ receives type STRING because it is enclosed by quote characters. (Technically speaking these languages’ literals are monomorphic.) But this is not the only way to do this.
In more elaborate languages with type classes like Rust or Haskell, constant literals do not have intrinsic types and instead only receive a type when they are assigned to (or used as argument to) a context that demands a particular type. The way this works is that the language places these literals in a “class” of many possible types that the literal value could be interpreted as, and the literal stays there until context restricts the class further. (These languages handle literals as if they were polymorphic even though they eventually become monomorphic after constant folding.)
The benefit of this approach is that a literal that looks like one type can be freely used in a context that requires another type without the need for an implicit coercion. Some members in our team knew this from previous experience with other languages. Incidentally, Go has a very similar concept which it refers to as untyped constants, so our team of Go programmers was comfortable with this idea. So we decided to reuse this principle in CockroachSQL.
Yet that wasn’t enough, because we also wished our typing rules to accept constructs like INSERT INTO foo (float_col) VALUES (2 + 3).
With implicit type selection activated only for literals, the typing rule for “+” would see two arguments that have many possible types and bail out with an ambiguity error. Even if we had thought of implementing some sort of “ranking” of overloads based on argument types (a terrible idea, but bear with us for the sake of this example), this would not be sufficient since the best ranking would likely select the variant returning INT and then the INSERT would reject inserting an integer into a FLOAT column.
Instead, we generalized the typeclass-based handling of constant literals to any composite expression involving only constant literals as leaves and operators for which we can compute a result that would be valid in all the possible types chosen by the context. For this, we observed that we can perform nearly all number arithmetic in a suitably chosen representation that always computes numerically exact results, like the type Value provided by Go’s Constant package (used by the Go compiler for Go constant literals); doing what we wanted was simply a matter of integrating constant folding in an early phase of our algorithm.
To summarize, we knew early on that the key features of our typing algorithms would be:
- Constant folding in an exact type to delay typing constant literals as much as possible
- Inferring placeholder types based on their context
- Resolving overloads based on argument types
Design iterations
Early attempts: Rick & Morty
Our first design for a “new type system” was relatively complicated. Its design is fully described here; the salient feature is that it would go through multiple traversals of an expression tree containing placeholders until it could find a satisfying types for all placeholders, or detect that it is unable to make progress and then abort with an ambiguity error. This complexity appeared because we thought we wanted to solve the following use case:
Suppose three functions f, g and h each have 2 overloads, as follows:
f:int,float->int f:string,string->int g:float,decimal->int g:string,string->int h:decimal,float->int h:string,string->int
Given this, the problem was to infer types for the the placeholders in the expression “f($1,$2) + g($2,$3) + h($3,$1)”. With a naive algorithm, there is not enough information locally to each of the three individual function calls to infer a specific type for each placeholder. With the new design – an iterative algorithm – we could infer STRING for $1, $2 and $3 correctly.
However, of course, an iterative algorithm wasn’t satisfactory; we felt typing ought to be linear with respect to the size of the syntax. Also, truth be told, the driving examples were relatively far-fetched and rather unrealistic.
Then we thought about another design which wasn’t iterative and which would instead use heuristics to make things work in most cases even though it would fail in more complex (unrealistic) situations, like the one just above. This second design is detailed here. Since this was rather different from our previous idea, we wanted to differentiate them during technical discussions, and thus we chose the names “Rick & Morty” for first and second designs respectively.
We described both in our typing RFC and stated our preference for Morty. The RFC was discussed with the team, accepted, and then awaited implementation.
When Nathan began implementing the new CockroachSQL type system, something unexpected happened. He thought he was implementing Morty, but when he explained his new system we realized he actually had implemented something else entirely. In strict engineering terms, this could have been interpreted as an error, as his implementation diverged from the spec; however we were quick to realize his implementation was much better than Morty (and Rick) [1]: it could type most SQL queries we were interested about with a simpler set of rules than Morty (and thus Rick).
And so did we rediscover that Worse is Better.
[1] There is a lesson here about the relative order of specification RFCs and their implementation. We learned from experience.
Summer: Bi-directional typing with untyped constant literals
CockroachSQL’s new type system is called “Summer,” after Morty’s sister in the eponymous show.
Summer fits the requirements set forth earlier, by integrating early constant folding; typeclass-based inference of constant literals; bottom-to-top typing; and extra logic for overload resolution and homogeneous typing.
Summer’s salient feature is how it solves ambiguity.
In a twist to our requirement for bottom-to-top typing, Summer’s typing algorithm propagates a type “preference” down the recursion (as input to the recursive step) decided by an expression’s parent node. This enables Summer to infer the desired types of constant values in SQL queries based on how that constant gets used. We were surprised and happy to find that this simple mechanism resolves ambiguity in most interesting cases, without the complex rules or heuristics needed by Rick and Morty to achieve the same. Furthermore, we confirmed that this approach obviates the need to introduce implicit coercions during type checking.
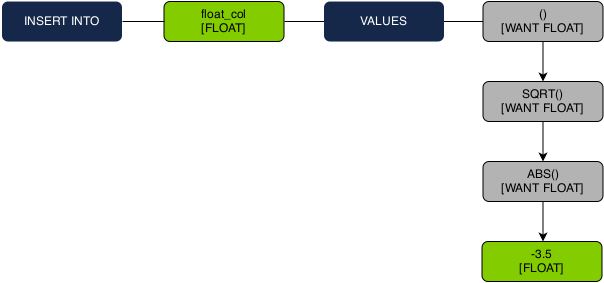
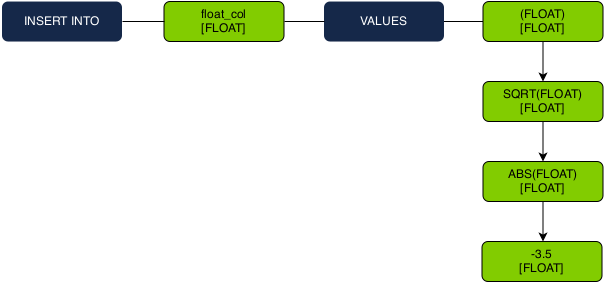
Let check out how these new rules play together when typing the query:
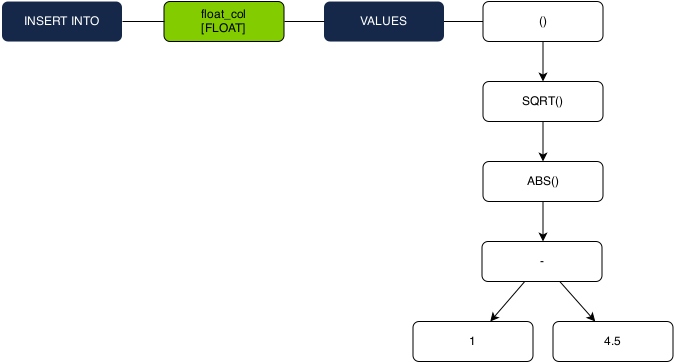
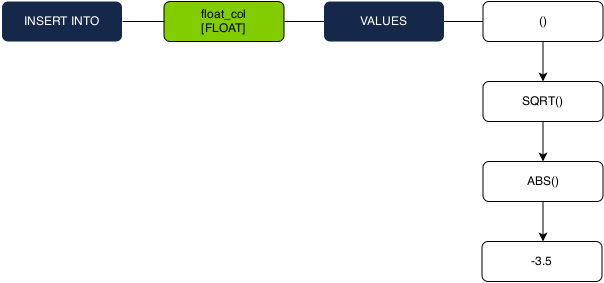
INSERT INTO float_col VALUES (SQRT(ABS(1-4.5)));
1. Before type checking begins, we fold all constant operations using exact arithmetic.
2. We then propagate the desired FLOAT type down the expression tree during the type checking recursion.
3. -3.5 is a constant so we check that FLOAT is in its resolvable type set. Because it is, we resolve the constant as a FLOAT datum type.
4. As the recursion goes back up, we have a pair of straightforward overloads that are resolved to their FLOAT implementations.
5. The entire expression is resolved to a FLOAT, which matches the insert column type.
To give more insight into the intermediate and final types during type checking, we also added a new EXPLAIN mode called EXPLAIN(TYPES). In this mode, EXPLAIN shows the types of all sub-expressions involved in a statement, as well as the derived types of result columns in each intermediate step of the query plan. If we run this explain mode on the previous query, we get:
> EXPLAIN (TYPES) INSERT INTO float_col VALUES (SQRT(ABS(1-4.5))); +-------+--------+---------------+-----------------------------------------------------------------+ | Level | Type | Element | Description | +-------+--------+---------------+-----------------------------------------------------------------+ | 0 | insert | result | () | | 1 | values | result | (column1 float) | | 1 | values | row 0, expr 0 | (SQRT((ABS((-3.5000000000000000)[float]))[float]))[float] | +-------+--------+---------------+-----------------------------------------------------------------+
For most expression types, Summer is a seamless extension of CockroachDB’s original type system. For instance, the AND expression now passes down a desired type of BOOLEAN during the downward pass into both its left and right subexpressions. Then, during the upward pass, the AND expression asserts that each subexpression did in fact type itself as a BOOLEAN, throwing a typing error if not, and typing itself as a BOOLEAN if so.
Beyond the mechanism of “preferred” types, Summer provides straightforward rules for required homogeneity and overload resolution.
Type inference for functions requiring homogeneous arguments
Summer defines rules for how to determine a mutually-shared type, given an arbitrary set of expressions. This primitive comes into play for a number of classes of expressions:
COALESCE: all parameters need to be the same typeCASE: all conditions need to be the same type and all values need to be the same typeNULLIF: both subexpressions need to be the same typeRANGE: all three subexpressions need to be the same type- A few other expression types…
To support type inference in all of these cases, we built a set of rules that can be applied to determine the homogeneous shared type for a set of expressions. To see these rules in play, let’s inspect how we would handle the following SQL query:
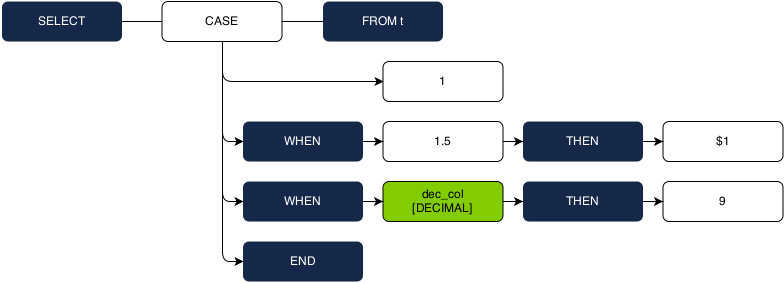
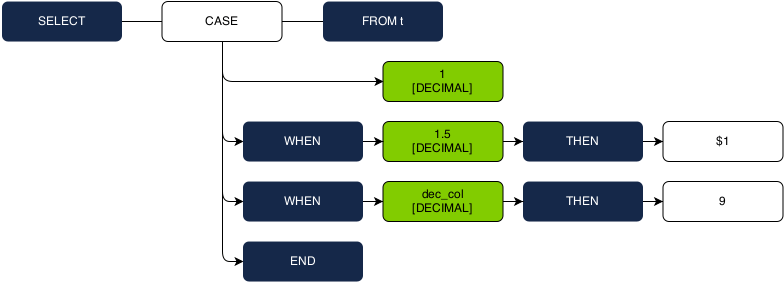
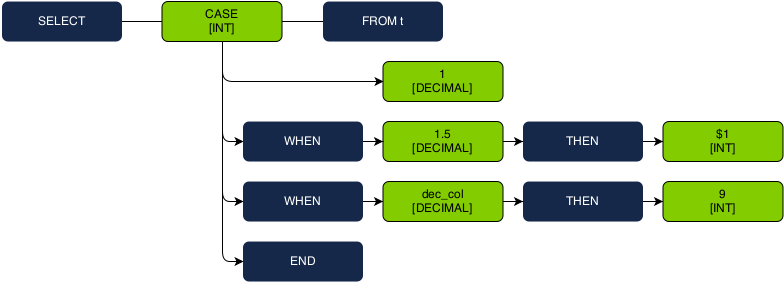
SELECT CASE 1 WHEN 1.5 THEN $1 WHEN dec_col THEN 1 END FROM t;
1. First look at the input and WHEN expressions, which must all be a homogenous type. This set of expressions includes two constant literals (‘1’ and ‘1.5’) and the column reference ‘dec_col’, which is referencing a column with the type decimal.
2. Because ‘dec_col’ can only be used as a decimal, we verify that DECIMAL is in the resolvable type set of the two constants. Because it is, we are able to infer that all three values have a type of DECIMAL.
3. Next, we look at the two THEN expressions, which also much all be a homogeneous type. The placeholder ‘$1’ has all types in its resolvable type set, so it exerts no preference for the shared type. If the placeholder was alone here, we would have to throw an ambiguity error.
4. However, the placeholder must have the same type as the literal value ‘9’. This value has a natural type of INT, so INT is assigned for both of their types, and is propagated up as the return type of the entire CASE expression.
Again, we can see this rule in action if we use Explain(TYPES):
> EXPLAIN (TYPES) SELECT CASE 1 WHEN 1.5 THEN $1 WHEN dec_col THEN 1 END FROM t;
+-------+---------------+----------+-------------------------------------------------------------------------------------------------------+
| Level | Type | Element | Description |
+-------+---------------+----------+-------------------------------------------------------------------------------------------------------+
| 0 | select | result | ("CASE 1 WHEN 1.5 THEN $1 WHEN dec_col THEN 1 END" int) |
| 1 | render/filter | result | ("CASE 1 WHEN 1.5 THEN $1 WHEN dec_col THEN 1 END" int) |
| 1 | render/filter | render 0 | (CASE (1)[decimal] WHEN (1.5)[decimal] THEN ($1)[int] WHEN (dec_col)[decimal] THEN (1)[int] END)[int] |
| 2 | scan | result | (dec_col decimal) |
+-------+---------------+----------+-------------------------------------------------------------------------------------------------------+
Type Inference of function calls and Overload Resolution
Summer also provides rules for determining which function to choose when given a set of candidate overloads. This is critical, because many functions in SQL are overloaded to support multiple types of inputs. On top of this, unary operations, binary operations, and comparison operations all require some form of overload resolution to decide which runtime implementation of them to use.
Flexibility
While Summer does not support implicit type casts, it does provide an improved level of flexibility through type inference without compromising on clarity. A recent change we made exemplifies this point. After the completion of Summer, we received a request to allow implicit casts between TEXT and TIMESTAMP values. The use case driving this proposal was a simple query:
INSERT INTO ts_col VALUES ('2016-5-17 18:22:4.303000 +2:0:0');
Implicit casts were a specific anti-goal of our type system, but we also realize that our type system could fully support this class of query. Instead, all we needed to do was to extend the type class of constant literal strings to include the TIMESTAMP type. In fact, following this train of thought, we extended their type class to include DATE and INTERVAL as well. With this small extension, string literal values which can become one of these types during type resolution are now allowed to be interpreted as their context demands.
Types and performance
Intelligent typing is not only a matter of improving the experience of programmers writing SQL queries. It’s also about providing the query engine with the right information to choose a good query plan. Consider for example a table with a column initially defined as floating point:
> CREATE TABLE Item (length REAL, desc TEXT); > CREATE INDEX lIdx ON Item(length);
Using this schema, let’s investigate the query plan for a query like the following:
> EXPLAIN SELECT desc FROM Item WHERE length = 3.5; +-------+------+------------------------------------+ | Level | Type | Description | +-------+------+------------------------------------+ | 0 | scan | Item@lIdx /3.5-/3.5000000000000004 | +-------+------+------------------------------------+
We can confirm that the engine properly selects lIdx for the lookup. (EXPLAIN’s output is explained in a previous blog post.)
Now suppose that as this application lives on, it appears that most items in this database actually have lengths that are round (integer) numbers. It may then look interesting to change the DB schema to use the type INT for the “length” column without having to change the client, so as to conserve time (INT comparisons are cheaper). After all, if the client only provides round number for lookups, the query engine should “know” that the constant round value is really an INT and use the index, right?
We can investigate the query plan for the modified schema and query:
> CREATE TABLE Item (length INTEGER, desc TEXT); > CREATE INDEX lIdx ON Item(length); > EXPLAIN SELECT desc FROM Item WHERE length = 3.0; +-------+------+-------------+ | Level | Type | Description | +-------+------+-------------+ | 0 | scan | Item@lIdx - | +-------+------+-------------+
What gives? CockroachDB, prior to Summer, did not (and could not) consider heterogeneous comparisons as a candidate for index selection. So when the value “3.0” would get typed as REAL, the comparison in the WHERE clause was heterogeneous and the query planner would choose (unfortunately) a full index scan with post-scan filtering. (And incidentally, so do several competing DBMS, too; some even don’t use an index at all.) This problem, in general, offsets the benefits of schema changes to exploit application-level knowledge about actual values until clients are modified to use the updated column types too.
With the new Summer type system, the constant 3.0 is interpreted using the type demanded by its context, and is simplified to an INT before index selection because representing 3.0 as an INT is possible without truncation or rounding. The query is thus optimized again, preserving the lookup time complexity of the table prior to the schema change. The benefits of the schema change are thus fully exploited without changes to client code and queries.
To summarize, we’d like to offer the thought that CockroachDB makes it easier to write complex WHERE clauses on columns of various types using arbitrary literal formats, because the query optimizer won’t need to consider under which circumstances the database knows how to convert constant literals.
What’s next for Summer
Summer, CockroachDB’s new type system, is now implemented and available for use. You can even explore how it behaves with your SQL code using the EXPLAIN(TYPES) statement.
We are continuing to improve the SQL implementation in CockroachDB, and a big part of that work will include refining our type system. So far we have already confirmed that our typing rules behave adequately for a variety of SQL benchmarks and reference test suites, including SQLLite’s Sqllogictest. We do have a few minor deviations (such as our number division returning DECIMAL even for integer operands) but they are deliberate choices for CockroachDB rather than unavoidable limitations of our type system.
In the coming months, we will invest in ensuring CockroachDB can be used from popular ORMs, and we intend to adapt our typing rules as far as necessary to make these tools happy. While holding on to our goal of straightforward rules and no surprises, we will continue to iterate on making our type system even more usable and expressive.
If distributed SQL makes you giddy, check out our open positions here.